|
Zahlen Die natürlichen Zahlen sind bekannt {1,2,3,4,5,6,7,8,9,10,11,...}Man kann die natürlichen Zahlen nach bestimmten Eigenschaften untersuchen. Etwa die geraden natürlichen Zahlen {2,4,6,8,10,12,...} Diese kann man beschreiben durch a=2.b (eine gerade Zahl ist das doppelte einer anderen natürlichen Zahl). Oder die ungeraden natürlichen Zahlen {1,3,5,7,9,11,...} Diese kann man beschreiben durch a=2.b+1 (eine ungerade Zahl ist das doppelte einer natürlichen Zahl plus 1) sowie die Zahl 1 selbst. Dann kann man Aussagen machen: Die Multiplikation zweier gerader natürlicher Zahlen ist wieder eine gerade Zahl. Beweis: Man bezeichne die beiden gegebenen geraden Zahlen mit a und e. Dann gibt es andere natürliche Zahlen b und f mit a=2.b und e=2.f, dann a.e=2.b.2.f und weil b.2.f eine natürliche Zahl ist und das doppelte davon a.e ist so ist a.e eine gerade Zahl. Die Multiplikation zweier ungerader natürlicher Zahlen ist wieder eine ungerade Zahl Beweis: Man bezeichne die beiden gegebenen ungeraden Zahlen mit a und e. Dann gibt es andere natürliche Zahlen b und f mit a=2.b+1 und e=2.f+1, dann a.e=(2b+1).(2f+1)=2(b.2.f+f+b)+1 und weil (b.2.f+f+b) eine natürliche Zahl ist und das doppelte davon +1 das Produkt a.e ist, so ist a.e eine ungerade Zahl. Oder es gibt natürliche Zahlen mit 3²+4²=5² 6²+8²=10² 5²+12²=13² usw. Dies erinnert sofort an den Satz des Pythagoras und man kann daher eine Schnur markieren mit zunächst 3 Einheiten, anschießend 4 Einheiten, anschließend 5 Einheiten. Hält man dann an den Übergangsstellen fest und zieht ein Dreieck auf, so kann man dadurch mit einfachen Mitteln einen rechten Winkel erzeugen. Oder die natürlichen Zahlen in Faktorzerlegung aufschreiben 2=2.1 3=3.1 4=2.2.1 5=5.1 6=3.2.1 7=7.1 8=2.2.2.1 9=3.3.1 usw. Zahlen die nur als Produkt von sich selbst und 1 dargestellt werden können heißen Primzahlen. Und Primzahlen spielen die entscheidende Rolle bei der Daten-Verschlüsselung im Internet. Aber eine Gleichung 2.a=1 läßt sich im Rahmen der natürlichen Zahlen nicht lösen. Also erweitert man die Zahlen durch Brüche. Ein Bruch hat die Form a/b wobei a und b natürliche Zahlen sind und man kann diese Bruch-Zahlen auch als Komma-Zahlen aufschreiben. Damit kann man die Verhältnisse bei Strahlensatz und Dreisatz gut bearbeiten. Jeder Taschenrechner und jeder Computer arbeitet alleine mit Bruch-Zahlen und jede auf Papier aufschreibbare Zahl ist eine Bruch-Zahl. Zwischen zwei Bruch-Zahlen kann man beliebig viele weitere Brüche erzeugen. Und man kann sich fragen ob es denn zwischen den beliebig dicht gepackten Brüchen nicht doch noch Lücken gibt, also Zahlen die nicht durch einen Bruch dargestellt werden können. Die Entdeckung daß es solche Lücken-Zahlen gibt hat in der Geschichte ein ganzes Weltbild ins wanken gebracht. Und man kann sogar sagen: es gibt mehr Lücken-Zahlen als es Bruch-Zahlen gibt. Ein einfaches Beispiel ist die Lösung der Gleichung x²=2 Angenommen das gesuchte x ist ein Bruch, also darstellbar durch n/m mit natürlichen Zahlen m und n die man als teilerfremd annehmen kann (denn sonst kürzt man diese ganz fix). Dann folgt durch Quadrieren n.n=2.m.m Also ist n.n eine gerade Zahl. Und nach obiger Betrachtung über gerade Zahlen muß auch n eine gerade Zahl sein (wenn n ungerade wäre so wäre auch n.n ungerade). Also gibt es eine natürliche Zahl g mit n=2.g und damit 2.g.g=m.m Das heißt aber wiederum daß m.m eine gerade Zahl ist und somit auch m eine gerade Zahl ist (wenn m ungerade wäre so wäre auch m.m ungerade) Damit wäre n/m nicht teilerfremd, sondern durch 2 zu kürzen. Also kann es einen solchen Bruch als Lösung von x²=2 nicht geben. Aber man kann sich der Lösung annähern und zwar beliebig genau. Man gibt dieser Lösung einen Namen Man kann sich y=x² im Schaubild ansehen |
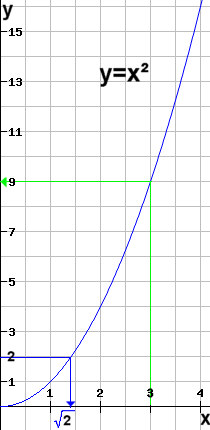
| Es gibt eine eindeutige
Zuordnung von einer auf der y-Achse ausgewählten Zahl zu der
entsprechenden Zahl auf der x-Achse im Bereich der positiven reellen
Zahlen. Dieser Zuordnung gibt man die Bezeichnung Wurzel und soll auf dieser Seite generell als blaue Wurzel geschrieben werden. Nun kann man Zahlen betrachten in der Form 0,1 0,01 0,001 0,0001 0,00001 0,000001 0,0000001 usw... Diese Zahlen erlauben die beliebig genaue Berechnung einer Zahl die es hier auf dieser Seite noch nicht gibt, eine beliebig kleine Zahl. Dieser ist die Bezeichnung 0 gegeben worden. 0 kann beliebig genau berechnet werden und ist folglich eine reelle Zahl. Welche Eigenschaften hat diese Zahl: Addiert man zu irgendeiner Zahl a eine beliebig kleine Zahl so erhält man eine beliebig genaue Berechnung von der Zahl a selbst, also a+0=a Multipliziert man irgendeine Zahl a mit einer beliebig kleinen Zahl so wird auch dieses Produkt beliebig klein, also a.0=0 Bei der Division einer Zahl a erhält man aber a:0,1=10.a a:0,01=100.a a:0,001=1000.a usw... Die Zahl explodiert also und wächst über alle bekannten Grenzen. Es gibt kein sinnvolles Ergebnis für das Teilen durch 0. Daher wird das Teilen durch 0 verboten. Aber eine Gleichung 2+a=0 läßt sich im Rahmen der positiven reellen Zahlen nicht lösen. Also erweitert man die bisherigen positiven Zahlen durch die negativen reellen Zahlen, die die Beziehung a+(-a)=0 erfüllen. Damit hat man die normalerweise bekannten reellen Zahlen mit ihren Rechenregeln.Z.B. |
| 4-4=4-4 | dann auf der linken Seite 2 ausklammern |
| 2(2-2)=4-4 | dann auf der rechten Seite verwenden (a+b)(a-b)=a²-b² |
| 2(2-2)=(2-2)(2+2) | dann teilen durch (2-2) ergibt |
| 2=(2+2)=4 |
| Hier ist die Regel verletzt
worden daß das Teilen durch 0 verboten ist. Ein Nicht-Beachten dieser Regel führt zu Widersprüchen. Es ist immer zu prüfen ob der Teiler nicht 0 ist. Und das ist manchmal gar nicht so einfach: |
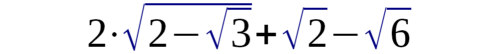
| Oder weiß man hier sofort
ob dieser Ausdruck 0 ist oder nicht? Ein anderes Beispiel |
![]()
| Bei den reellen Zahlen (positive und negative) ist die Wurzel aus x so definiert daß das Quadrat davon wieder x ergibt. Man kann sich das im Bild ansehen |
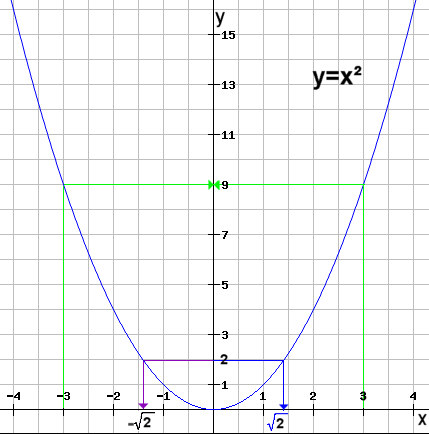
| Hier sieht man daß zu einer
positiven reellen Zahl auf der y-Achse zwei Lösungen mit diesen
Eigenschaften existieren. Man könnte schreiben Dabei ist die blaue Wurzel die eindeutig bestimmte Wurzel in den positiven reellen Zahlen und die schwarze Wurzel die verallgemeinerte Wurzel in den positiven und negativen reellen Zahlen. Genau genommen sind dies verschiedene Wurzeln die nur übereinstimmen wenn man alleine positive reelle Zahlen zugrundelegt. Damit schreibt sich das letzte Beispiel |

| Dies ist eine wahre Aussage
aber man kann daraus NICHT schließen daß -4=+4 gilt. Wenn Peter,
Jan, Hans, Elemente der Skatabend-Menge sind, so kann man aus Peter ist
Element der Skatabend-Menge nicht schließen daß Peter=Hans ist. Die Gleichheit bei der verallgemeinerten Wurzel bedeuted eine Gleichheit der Lösungsmengen. Einfacher ist es bei x³. Man kann sich das Schaubild ansehen. Es gibt für alle reellen Zahlen immer eine eindeutige Lösung für die Umkehrfunktion |
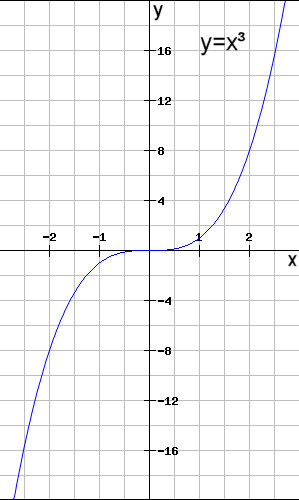
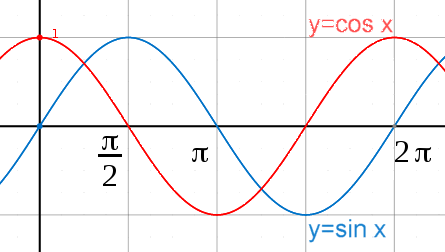
| Anders ist es dagegen bei sin(x) bei der die Umkehrfunktion (bei einem y-Wert zwischen +1 und -1) eine Lösungsmenge von unendlich vielen Elementen besitzt. |
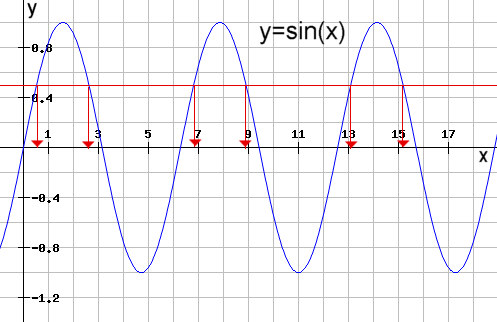
| Daher weiß man schon was
bei dem nächsten Beispiel falsch läuft (Wenn Peter, Jan, Hans, Elemente der Skatabend-Menge sind, so kann man aus Peter ist Element der Skatabend-Menge nicht schließen daß Peter=Hans ist) |

| Innerhalb der reellen Zahlen
gibt es keine Lösung der Gleichung x²= -1 Also erweitert man die Zahlen indem man eine neue Zahl i definiert für die i²= -1 gesetzt wird. Man erhält die komplexen Zahlen in der Form K= a + b.i mit reellen Zahlen a und b Die Erweiterung der positiven Zahlen durch Hinzunahme der negativen Zahlen hat bei geometrischen Überlegungen und bei Längenberechnungen keine Bedeutung aber bei Geldberechnungen hat man es mit Guthaben und Schulden zu tun und die negativen Zahlen sind dafür unerläßlich. So haben auch die neu hinzugenommenen komplexen Zahlen ihre Berechtigung bei mathematischen und anderen wissenschaftlichen Überlegungen. Die Umkehrfunktion |

| Die Mehrdeutigkeit der
Lösungen im Komplexen ist also stärker vorhanden als im Reellen und daher weiß man schon was
bei den nächsten Beispielen falsch läuft (Wenn Peter, Jan, Hans, Elemente der Skatabend-Menge sind, so kann man aus Peter ist Element der Skatabend-Menge nicht schließen daß Peter=Hans ist) |
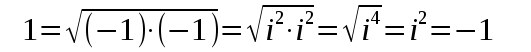
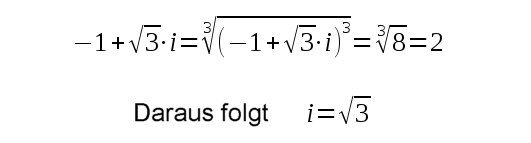
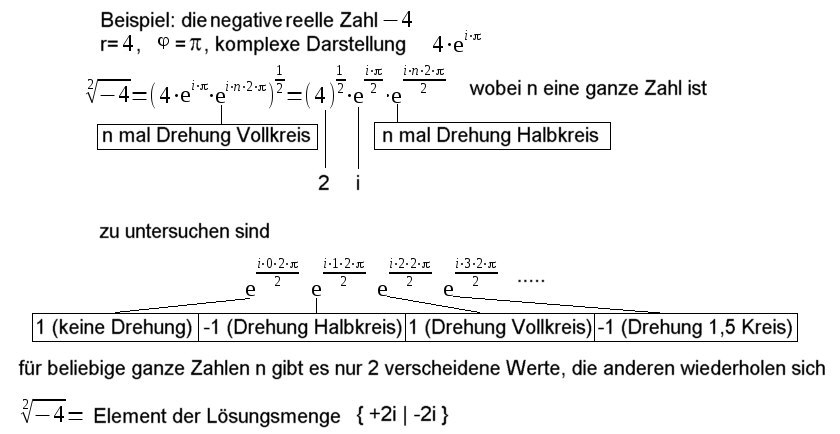
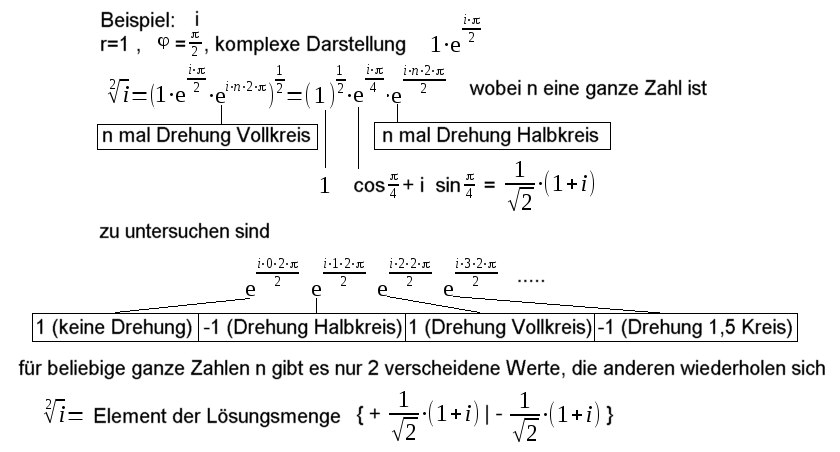
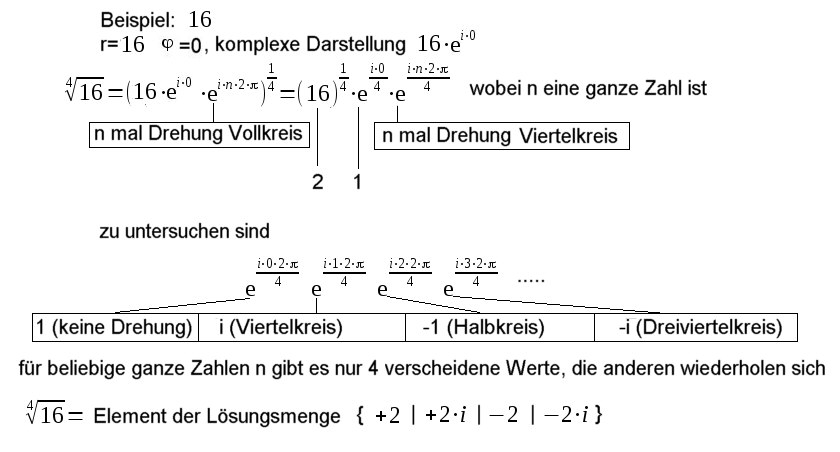
| Man kann sich über die Mehrdeutigkeit bei komplexen Zahlen eine bessere Übersicht verschaffen durch Umformung in die Polarform. |
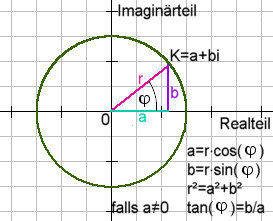
| Der Winkel Bei Bei Bei Bei Bei |

| Die Lösungsmengen bestimmen
sich durch |

| Manchmal ist es vorteilhaft sich auf z = a + b.i zurückzubesinnen und mit den reellen Koeffizienten a,b zu rechnen. Hier ein Beispiel zur Lösung einer komplexen quadratischen Gleichung. Gesucht sind alle komplexen Lösungen z der Gleichung: |
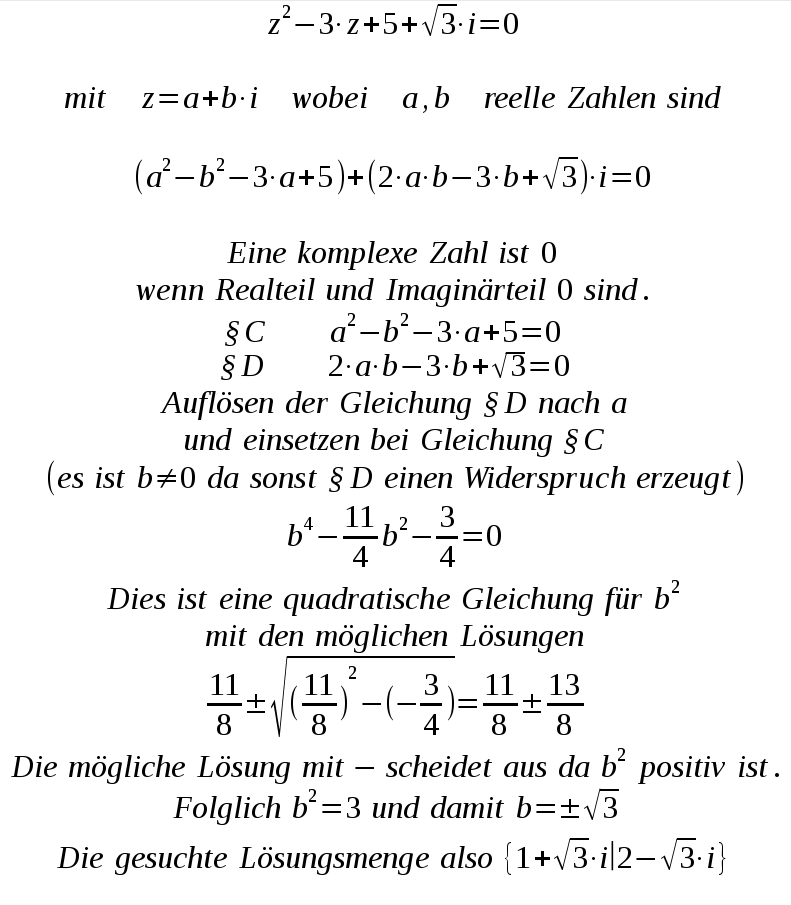

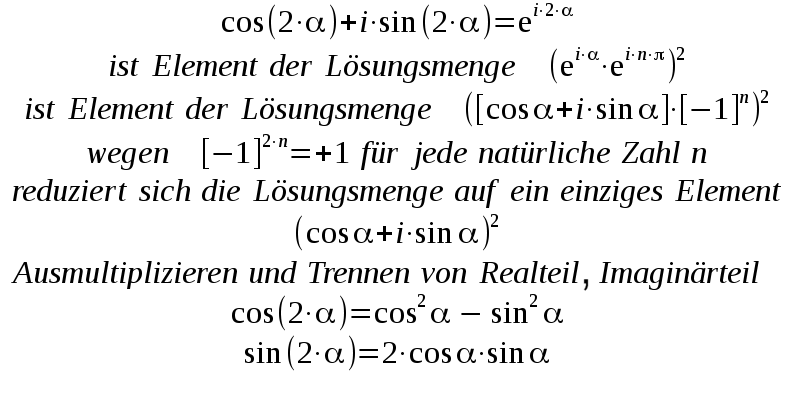
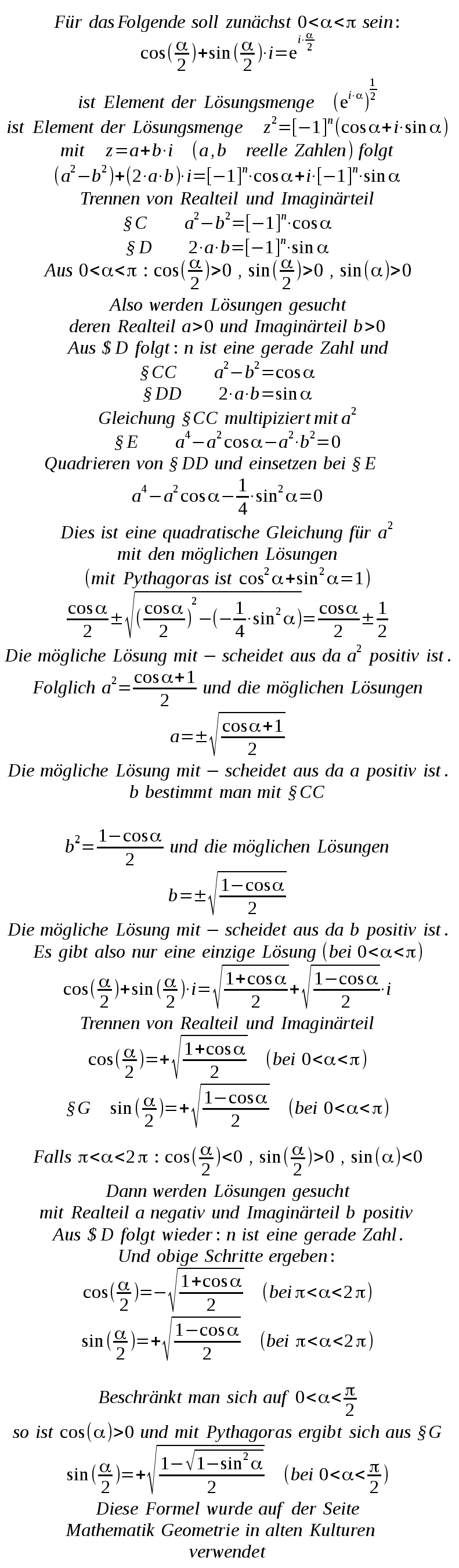
|
Komplexe Zahlen werden immer wieder als nicht real bezeichnet. Aber auch
die reellen irrationalen Zahlen könnten eigentlich als nicht real
bezeichnet werden. Denn sie lassen sich nur durch näherungsweise
Werte bestimmmen. Auch die negativen Zahlen wurden lange Zeit als nicht
real bezeichnet. Denn es gibt keine negativen Längen oder
Gewichte. Also sind vielleicht nur die natürlichen positiven Zahlen real? Nimmt man z.B. die Zahl 10, so ist der reale Bezug der daß es 10 gleiche Objekte gibt. Aber 100%-ig gleiche Objekte gibt es in der Realität nicht, jeder Stein ist anders, jeder Baum ist anders, jeder Mensch ist anders...! Die Zahl 10 ist also nicht real! Sie ist eine gedankliche Abstraktion. Jede auf irgendeine Weise gebildete Zahl ist eine gedankliche Abstraktion. Wichtig ist es die Verknüpfungsregeln von Zahlen zu kennen, z.B. Addition und Multiplikation, und die Gedankenvorstellungen die als Theorie-Netz über die Realität geworfen werden. So kann man eine Familie betrachten bestehend aus 10 Personen. Die Personen-Objekte sind nicht gleich, es gibt Männer, Frauen und Kinder, unterschiedliches Alter und Größe,...aber durch eine Eigenschaft abstrakt als Menge zusammengefaßt: Familie. Stirbt ein Familienmitglied so ist 10-1 zu bilden. Wird ein Kind geboren so ist 10+1 zu bilden. Angenommen diese Familie lebt auf einer Insel auf der 83 weitere Personen leben so kann man die Personenzahl beschreiben durch 10+83i (10 Familienangehörige plus 83 andere Inselbewohner). Wenn ein Ehepaar aus der Familie sich scheiden läßt so ist 10 ->9+i zu bilden: Die Scheidung wird durch einen Operator dargestellt der aus einer reellen Zahl eine komplexe Zahl (mit Realteil und Imaginärteil) macht. Wenn ein Familienmitglied eine andere Inselperson heiratet so ist 83i ->1+82i zu bilden: Die Heirat wird durch einen Operator dargestellt der aus einer rein-imaginären Zahl eine komplexe Zahl (mit Realteil und Imaginärteil) macht. Schon hat man komplexe Zahlen benutzt um Vorgänge in der Realität durch ein Theorie-Netz zu verbinden. |